FlareOn 8 - 0x2 - Known

Challenge

You are given an executable file (UnlockYourFiles.exe) and a list of encrypted files in the directory inside files. If you execute the .exe you’re asked to enter the decryption key: 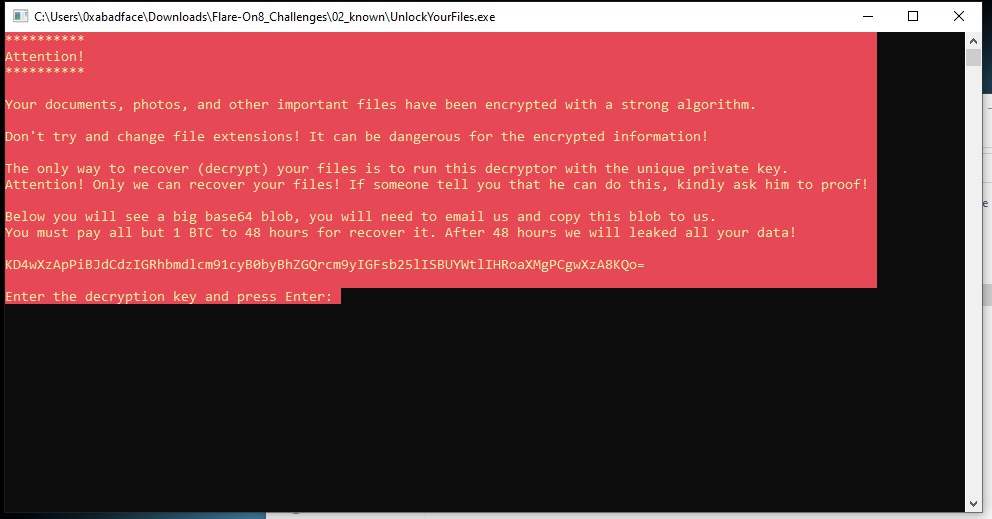… which obviously we don’t have.

Goal: find the decryption key to decrypt the files.

Solution

So, this must be some kind of (fake) ransomware logic hidden inside the exe. So, we open the executable inside IDA, showing the main following a few number of functions:

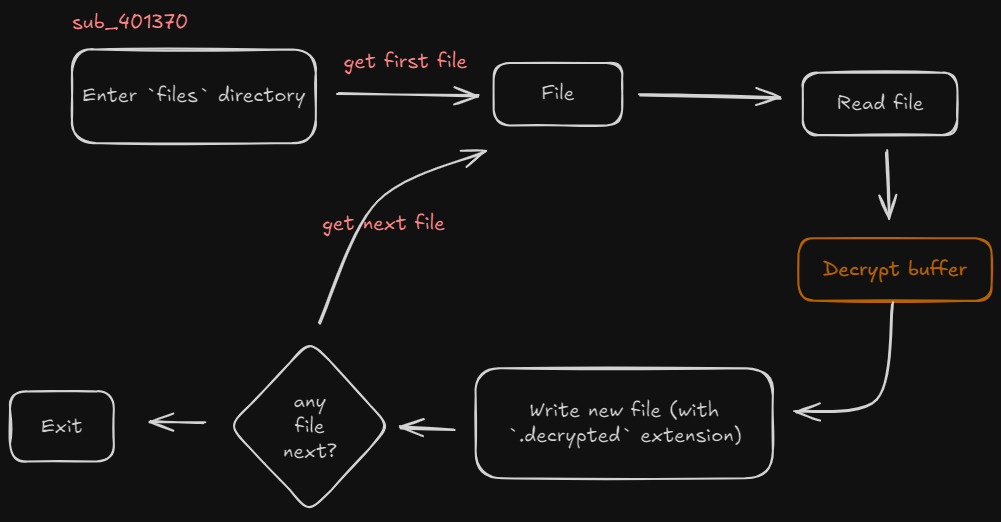
The Win32 APis FindFirstFileA, ReadFile , WriteFile are suspicious… somewhere between those is probably hidden the decrypting phase of the binary. I renamed all the functions leaving the offsets so you can understand which function I renamed. Roughly, the flow of execution is like this: The function that decrypts data is sub_FE11F0. Particularly, the algorithm receives an 8-byte block of data of the file at a time and decrypts it. Here’s shown the algorithm: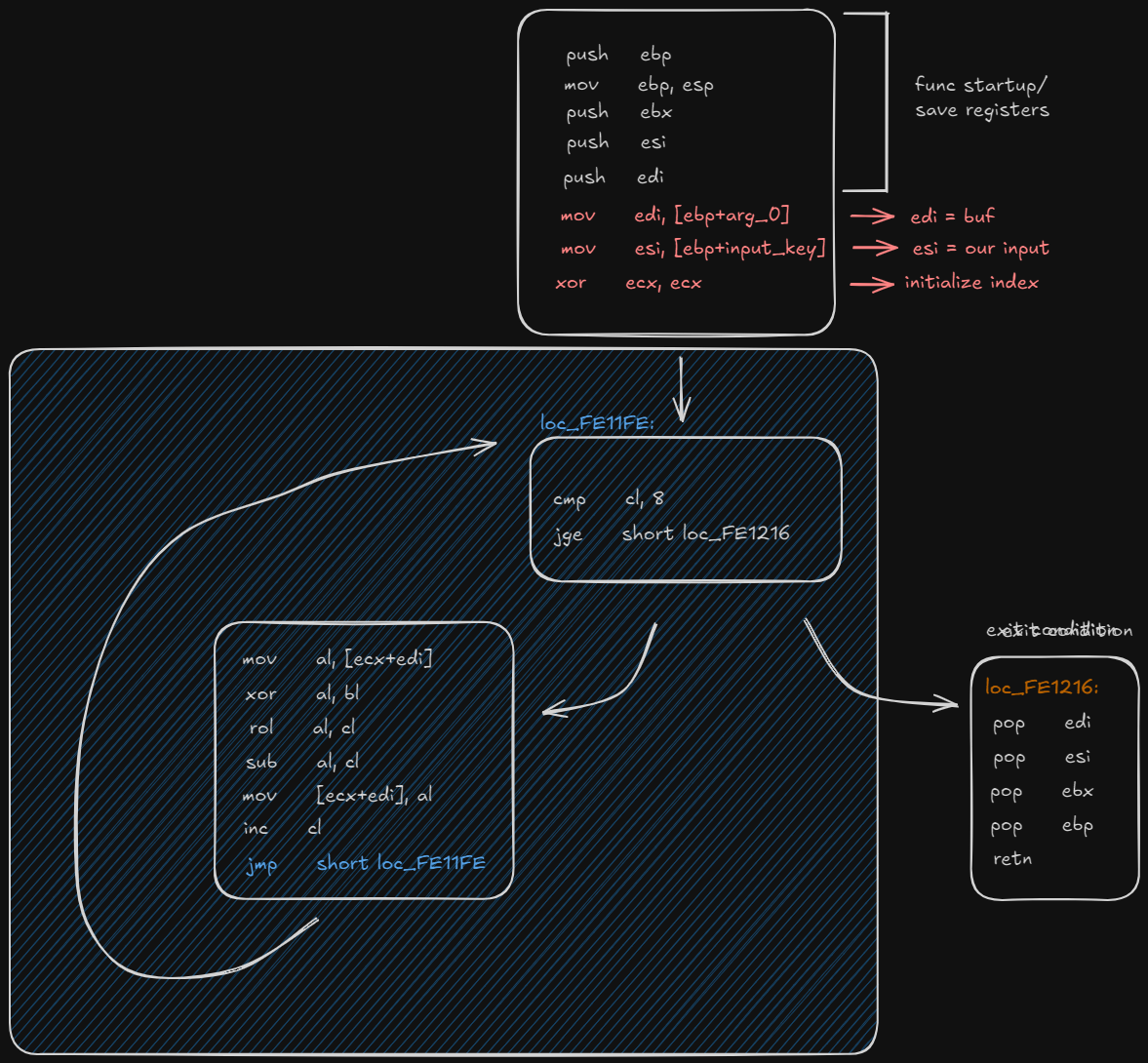 Inside the loop, each character of the input key is extracted and encrypted and put inside edi at index ecx. Another useless schema (because I like them) just to show an example: 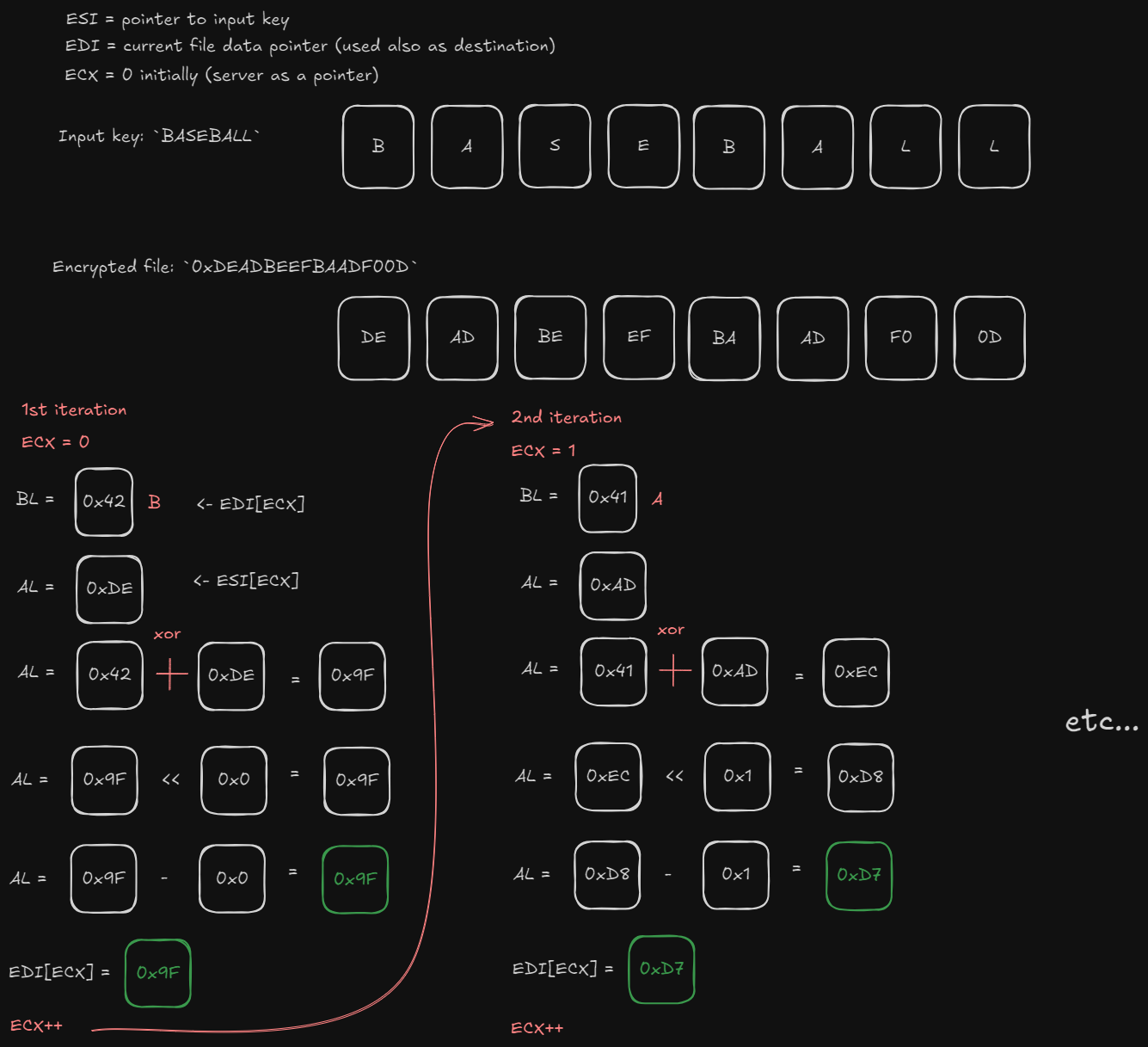So the first byte will be 0x9F, the second 0xD7…

Ok, but the key? We don’t have it!

Let’s see the encrypted files inside the files folder:

• capa.png
• cicero.txt
• commandovm.gif
• critical_data.txt
• flarevm.jpg
• latin_alphabet.txt

Some files make me wonder if I can use some known bytes from the lost original file, encrypt them and obtain the same result. Two of these files have the png and jpg extension, meaning that the original files were images. And what we know about image format? Each one of these image format has an header at the very start of the files, allowing software for recognizing and storing additional information. For example, the PNG has these sequence of bytes (pink):

JPGs instead use the JFIF (Jpeg File Interchange Format). As similar as PNG, it is composed by multiple sections, but we are interested on the start:

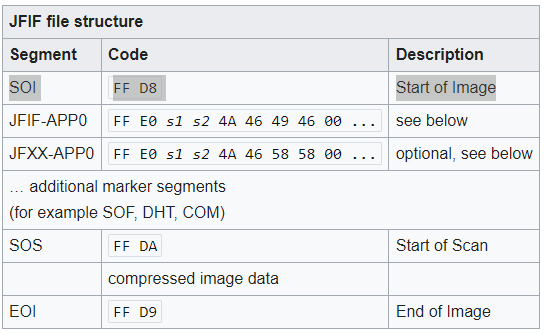
What we got?

• PNG header starting sequence: 89 50 4E 47 → (. P N G)
• PNG header starting sequence: FF D8

If we open capa.png with any hex editor, we find that the first bytes are C7 C7 25 1D. So, the original starting bytes 89 50 4E 47 were encrypted resulting into C7 C7 25 1D.

In cryptography there exist a particular attack called known plaintext attack. From wikipedia:

The known-plaintext attack (KPA) is an attack model for cryptanalysis where the attacker has access to both the plaintext (called a crib) and its encrypted version (ciphertext). These can be used to reveal secret keys and code books.

Seems the perfect one to use! We have access to some bytes of the plaintext got from the image headers and all of the encrypted ones.

Ok, one problem left: we need at least 8 bytes of plaintext.

For this, we can start taking the first known bytes of the PNG/JPG images and other bytes from the other sections. NOTE: keep track of the index at which are these other bytes! There’s an easier way to do this, using the file latin_alphabet.txt that probably was ABCDEFGH..., so we consider the first 8 bytes as the plaintext ABCDEFGH. The encrypted file has these bytes: 0F CE 60 BC E6 2F 46 EA.

---

/* ----- INIT BONUS ----- */

We can also obtain the reverse algorithm by looking at the code, using the example of the input key BASEBALL and the encrypted bytes DE AD BE EF BA AD F0 0D

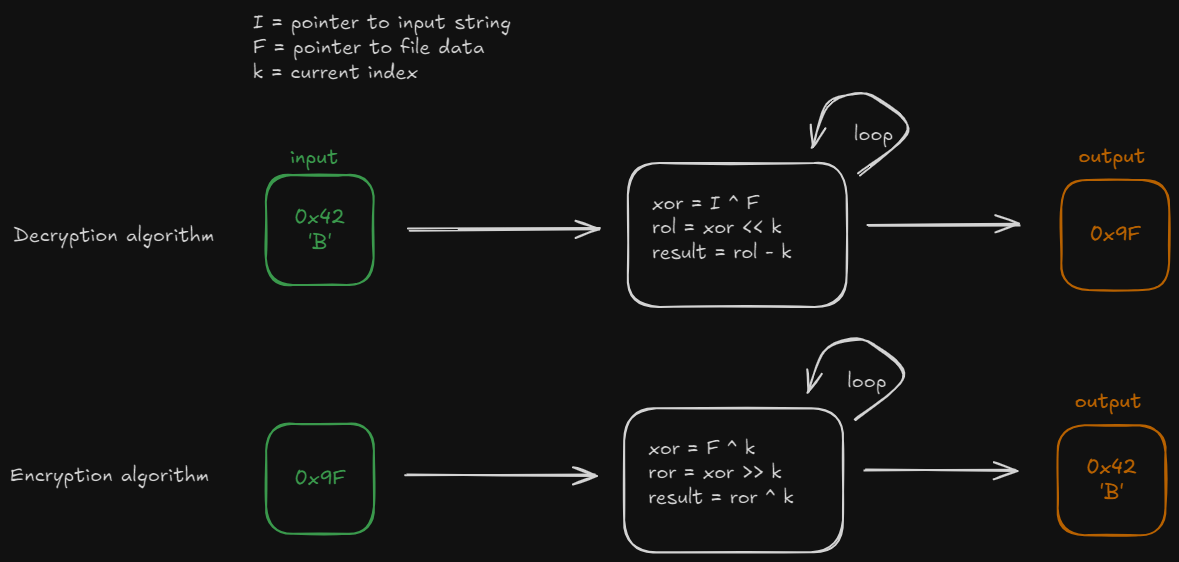
/* ----- END BONUS ----- */

---

Ok, recap on what we have

• 8-byte plaintext: ABCDEFGH
• 8-byte encrypted text: 0F CE 60 BC E6 2F 46 EA
• We know the algorithm - in this case, the decryption algorithm Unknown: the key.

How we can find the key? Maybe we can start trying out some combinations (?) Exactly yes!

In order to extract the key we can brute-force a byte in the range of [0x00, 0xFF] for each iteration and try to apply the decryption algorithm using this byte. If the decrypted text matches the expected one, we continue on the next iteration. That’s the script:

ROL = lambda val, r_bits, max_bits: \
    (val << r_bits%max_bits) & (2**max_bits-1) | \
    ((val & (2**max_bits-1)) >> (max_bits-(r_bits%max_bits)))
 
# Rotate right: 0b1001 --> 0b1100
ROR = lambda val, r_bits, max_bits: \
    ((val & (2**max_bits-1)) >> r_bits%max_bits) | \
    (val << (max_bits-(r_bits%max_bits)) & (2**max_bits-1))
 
max_bits = 8  # For fun, try 2, 17 or other arbitrary (positive!) values
 
def dec(c, kc, i):
    res = kc ^ c
    res = ROL(res,i, max_bits)
    res = res - i
    return res
    
 
def enc(c, kc, i):
    res = c ^ i
    res = ROR(res, i, max_bits)
    res = res ^ kc
    return res
 
 
def dump(s):
    return " ".join("{:02x}".format(ord(c)) for c in s)
 
if __name__ == "__main__":
    plain = "ABCDEFGH" # first 8 bytes of latin_alphabet.txt
    cipher = b'\x0F\xCE\x60\xBC\xE6\x2F\x46\xEA'
    
    print("Plaintext: \t\t\t{}".format([" ".join("{}".format(c) for c in plain)]))
    print(f"Bytes: \t\t\t\t{plain.encode().hex(' ')}")
    print("Encrypted ciphertext: \t\t{}".format(cipher.hex(' ')))
    
    i = 0
    res = ""
    for b in plain:
        for key in range(0x0, 0xFF):
            r = dec(cipher[i], key, i)
            if r == ord(b):
                print("Found key {} ({}) for {}".format(hex(key), chr(key), hex(r)))
                res = res + chr(key)
                i += 1
                break
                
    print(f"\nFound key {res}")

We just wait some clock cycles and…

PS C:\Users\0xabadface\Downloads\Flare-On8_Challenges\02_known > py .\dec2.py
Plaintext:                      ['A B C D E F G H']
Bytes:                          41 42 43 44 45 46 47 48
Encrypted ciphertext:           0f ce 60 bc e6 2f 46 ea
Found key 0x4e (N) for 0x41
Found key 0x6f (o) for 0x42
Found key 0x31 (1) for 0x43
Found key 0x54 (T) for 0x44
Found key 0x72 (r) for 0x45
Found key 0x75 (u) for 0x46
Found key 0x73 (s) for 0x47
Found key 0x74 (t) for 0x48
 
Found key No1Trust

The key is No1Trust. If we input this text into the binary we find that it correctly decrypted the files. If we look at critical_data.txt, it contains the flag: (>0_0)> You_Have_Awakened_Me_Too_Soon_EXE@flare-on.com <(0_0<)

---